< tHis Is yOungMusiC.oRg >

Scalesearch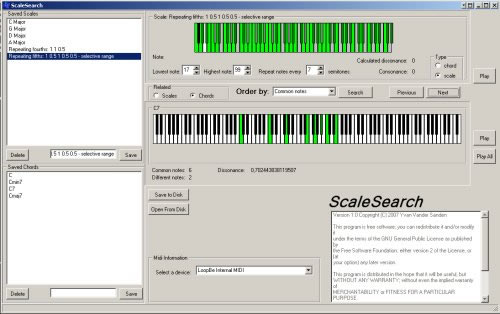

Download archive

A small tool which can be used to order chords or complex scales. I think it can be usefull to compare chords and scales on several criteria. For example, if you have a set of chords prepared for a composition (if you work that way, of course) you could easily see which are most or least related. Or in which of your selected scales a certain chord would fit most.

Some features

• Scales do not neccesarily use all octaves. You can set the lowest and highest note you want to work with.
• Scales do not have to repeat themselves. You can have different notes in every octave.
• Repeating scales can also be repeated every fourth, fifth or whatever you want.
• You can compare scales with scales, scales with chords, chords with scales and chords with chords.
• Common and different notes are calculated for every search.
• Degree of dissonance is calculated for every chord.
• Dissonance can be used to order chords in several ways.
• Chords and scales can be played through midi.

Most of the code is very straightforward. I wrote some libraries first to seperate the interface from the actual calculations. These libraries set up container objects for scales, chords and vectors of both. I think they are easy enough to understand to use in other software.

The code to calculate a chords' dissonance is mainly, but not entirely, borrowed from software on logosfoundation.org, written by G.W. Raes. Because it is quite important to know how this works if you want to know how the software works, I have included it below.

float cNoteContainer::freqToDissonance(float freq1, float freq2, float vel1, float vel2) {
  float centerFreq, bandFreq, diffFreq;
  float peak = 23; // peak frequency, see below
  float result   ;
  if ((vel1 + vel2) <= 1    ) return 0; // inaudible
  if (freq1         == freq2) return 0; // no dissonance in unisono

The function compares 2 frequencies and takes velocity into acount. The program actually does not only use the selected tones in a chord or scale, but also calculates a neutral range of the first 7 harmonics.

  if (freq1 > freq2) {
    swap(freq1, freq2);
    swap(vel1 , vel2 );
  }
   
  float weight = sqrt(vel1 * vel2)  / 127           ; // this is used for velocity   
  centerFreq   = sqrt(pow(freq1, 2) + pow(freq2, 2)); // central frequency for bandwith between these 2 
  centerFreq  /= 1000.0                             ; // convert to frequency    

  // The following is used to calculate the critical bandwith.   
  // Don't ask why. It works.   
  // if both tones are outside the critical bandwith around the   
  // center frequency, then there is no dissonance. 

  bandFreq = (6.23 * centerFreq * centerFreq) + (93.39 * centerFreq) + 28.52;

The central frequency is the average between two tones. If the tones are too far from each other. There is no dissonance.

  if (freq2 > (freq1 + bandFreq)) {
    return 0;   
  } else {
    // algorithm uses a triangular form with a peak at 23 Hz
    // at that point the dissonance is the most audible
    diffFreq = freq2 - freq1;
    if (diffFreq <= peak) result = diffFreq / peak;
    else                  result = peak / diffFreq;
  } 

Dissonance is at its 'best' at about 23 Hz. Higher and lower tones sound less dissonant together.

  return sqrt(pow(result, 2) * pow(weight, 2));   
}

If you have any questions about this program. Do not hesitate to ask. I will explain some more if needed.